Minecraft Redstone Tutorial: Half & Full Adders

Half and Full adders

Half adders are the combination of an XOR and an AND gate and they are the basis of binary addition (and as such of every other operation too).

Full adders are made up of two half adders combined in a specific way – the difference is full adders also consider a carry input.

Before getting into this, let’s explain a bit about binary and introduce a new gate: the XOR.

Binary format

In everyday life, we use the decimal system, which uses a total of 10 numbers: 0 to 9. This means that every number is the sum of a series of multiplications of powers of 10. For example, think of the number 384.

300 + 80 + 4
3*100 + 8*10 + 4*1
3*10^2 + 8*10^1 + 4*10^0

Notice that the exponents start at 0 and increase towards the left. Every time we add a digit, a new power of 10 is needed.

In binary, the system is based on the same principle, only instead of powers of 10 we use powers of 2. Let’s think of a small number to start with: 7.

4 + 2 + 1
1*4 + 1*2 + 1*1
1*2^2 + 1*2^1 + 1*2^0

There are only two possible numbers in binary: 0 and 1. The way you translate from decimal to binary is by finding what powers of two add up to that decimal number. 7 is made up of 2^1, 2^1 and 2^0, thus its binary equivalent is 111. Let’s see another example: the number 25.

16 + 8 + 1
1*16 + 1*8 + 0*4 + 0*2 + 1*1
1*2^4 + 1*2^3 + 0*2^2 + 0*2^1 + 1*2^0

Can you see the pattern? 25 in decimal is 11001 in binary, because we have one 16, one 8, zero 4s, zero 2s and one 1.

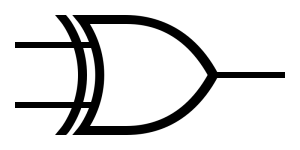
The XOR gate

You remember OR from a few posts ago? Now it’s time to study its more complicated brother, the Exclusive OR. This gate is often abbreviated as EOR, EXOR or XOR.

The output of an XOR gate is true only when exactly one of its inputs is true.

Here is the truth table:

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

The hardware representation:

Making it in Minecraft is slightly more complicated:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

Combining it all – making a half adder

A half adder is a mechanism that adds two bits. A bit is a binary digit, that is, a 1 or a 0.

Think of adding two numbers in decimal: if you want to add 15 and 37, you would:

Add 7 and 5, which gives you 12. 12 is not an atomic number, it is made out of 10 and 2.
You leave the 2 and carry the 10 over as a 1 to the next column.
You add the 1, the 3 and the 1 you just carried over to get 5.
You have your result: a 5 on the left and a 2 on the right, 52.

In other words, if your addition turns out to be bigger than 9, you turn it into a carry. The same thing happens in binary, only you use a carry whenever your sum is bigger than 1.

And how would you check your sum is bigger than 1? Well, the only way that can happen in binary is if you add a 1 and a 1: 1+1 = 10. We already have the perfect gate to detect this occurrence: an AND gate. Whenever both inputs are 1, the Carry output will turn on.

Any other situation is covered, again, by something we just saw, an XOR gate: 0 + 0 = 0, 1 + 0 = 1 and 0 + 1 = 1, however, 1 + 1 will do nothing, which is exactly what we want as it’s covered by the AND.

Now we just have to connect our inputs to our two gates, like in the following image. A and B are your inputs, S is the sum, C is the carry.

One possible Minecraft version:

1

2

3

4

5

6

Full adders

Full adders are a combination of two half adders that admit a carry input. In a real computer, the carry out of one full adder will be the carry in of the next full adder. This is their circuit diagram:

You should attempt to re-create the above with what you know without cheating, but if you get stuck, here is a very simple, uncompressed version of a full adder in Minecraft. With 4 of these chained as described above, you can create a 4-bit calculator – in other words, you can add numbers up to 2^4 or 16 inside Minecraft! You just have to translate them to binary first.

1

2

3

4

5

6

7

8

9

Half and Full adders

Binary format

The XOR gate

Combining it all – making a half adder

Full adders

Address

Map

Contact